Ecology: Biotic Potential & Overpopulation

INTRODUCTION

The growth of a natural population of organisms is a consequence of that particular organism’s biotic potential. Biotic potential is a consequence of reproductive factors that include age at sexual maturity, number of offspring produced per mating, number of matings per season, gestational period, nurturing period, & years of fertility.

Counteracting biotic potential is a variety of features in the environment that interact to suppress the growth rate & maximum size of a population. These features include those which are directly related to the density (# of organisms per unit of space) and are called density-dependent and others that are in effect regardless of the density which are known as density-independent.

Some density-dependent factors are predator/prey ratio, food supply, interspecific competition for an essential component of the environment, ability of the environment to absorb the wastes of the population, and the spread of pathogenic or parasitic organisms within the population. These problems get worse as the population density gets larger.

Density-independent factors include climatic changes and available cover as examples. Another example is a forest fire. Forest fires usually kill 30% of the organisms living in the forest regardless of the density of those organisms.

All of these combined make up the environmental resistance that a population encounters while trying to achieve the carrying capacity of an environment. The carrying capacity is the maximum number of individuals of a particular type that an environment can support indefinitely.

The human population was subject to the same factors of environmental resistance as other natural populations until very recently in the all too short history of humankind. We can assume that human beings, as we know them, have been around for at least 40,000 years. During this time, the world population managed to reach about 400 million by the year 1660. On October 12, 1999, the human population reached 6 billion. Today it is estimated that there are 6.6 billion people on earth. Thus, in less than 4 centuries, the human population has increased 14-fold in numbers over the growth that required nearly 40,000 years to achieve.

This has become known as the “population explosion”, and it is the result of a complex of accomplishments that have largely removed humankind from the influences of environmental resistance. These accomplishments include (1) becoming the top predator through the development of firearms, (2) the agricultural & industrial revolutions, and (3) the medical revolution. The agricultural and industrial revolutions are vulnerable to failure because they are both built on nonrenewable energy resources. The medical revolution has no restraints with respect to its impact on population growth. On the one hand, medicine continues to seek ways to make all couples fertile & keep all newborns alive, while on the other, it attempts to provide each human with as many additional years of life as is possible.

POPULATION GROWTH

The basic equation for calculating the growth rate of any population is given by:

Rate of increase Average births – Average deaths X existing

In numbers of = 100 population

Individuals

Thus, if a prairie dog town was known to contain 900 individuals, and the birth rate was 25 per 100 (25%) and the death rate was 12 per 100 (12%), then the rate of increase per year would be (0.25 – 0.12) X 900 = 0.13 X 900 = 117 more prairie dogs per year. At first, this seems like a phenomenal rate of growth. However, less than 150 years ago, our pioneer forefathers reported towns of prairie dogs (Cynomys ludovicianus) that occupied many square miles and contained millions of individuals!

Of course this kind of growth will encounter environmental resistance at some point (recall density-dependent & independent factors). We can include the effect of environmental resistance in our consideration of population increase by “establishing” a carrying capacity for our prairie dog environment. When we do this, our equation for determining the rate of increase in the number of individuals becomes:

Rate of increase carrying number of number of

In numbers of = births – deaths X capacity – individuals X individuals

Individuals 100 carrying capacity at any time

Let us now examine the growth of a population under more realistic circumstances in which we include the carrying capacity of the environment. We will use hypothetical data for the three phases through which any new population passes as it grows & determine the changes in the “rate of increase in the number of individuals” as the population progresses through each phase. Solve the above equation for the rate of increase using the data below.

MONTH POPULATION SIZE

0 Starting size = 20 dogs

Small size = 60 dogs

Small size = 90 dogs

Low middle size = 200 dogs

Middle size = 500 dogs

High middle size = 800 dogs

Low large size = 1000 dogs

Large size = 1250 dogs

32 High large size = 1450 dogs

To make the calculations, you will also need the following information:

Growth rate: 25 births per 100 and 12 deaths per 100 (as before)

Carrying capacity: 1500 prairie dogs.

Rate of increase carrying number of number of

In numbers of = births – deaths X capacity – individuals X individuals

Individuals 100 carrying capacity at any time

Let us perform the calculation of the first number of prairie dogs…

Rate of increase

In number of = (0.25 – 0.12) X 1500 - 20 X 20

Individuals 1500

= 0.13 X 1480 X 20

1500

= 0.13 X 0.99 X 20

= 2.6 dogs increase per unit of time when there are 20 dogs

Now, calculate the rate of increase in the number of individuals for the remaining 8 phases from the population data given above & record it in the table below.

Population Size as a Determiner of Increase in the Number of Individuals

Size (# of dogs)	Increase
20	2.6
60
90
200
500
800
1000
1250
1450

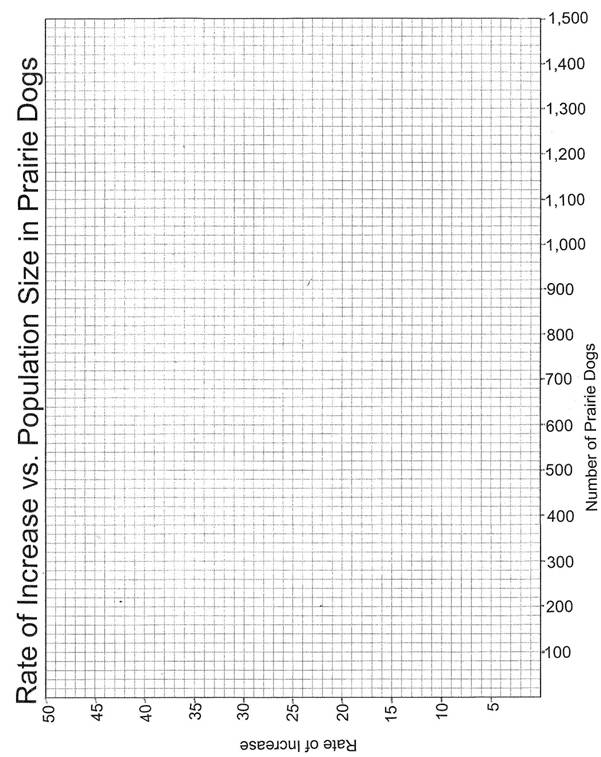
Turn the provided graph paper sideways & plot the rate of increase versus each size increment. The long horizontal axis (abscissa) represents the population sizes with one small square equivalent to 20 dogs, & the short vertical axis (ordinate) represents the increase in number for each population size with one small square equivalent to 1 prairie dog.

From your graph, when is the rate of increase the lowest? ________________________________________________________________

The most rapid? ________________________________________________________________

There is more than one time at which the rate of increase is slow. Explain the factors that are involved in causing these two periods of slow increase. It is important that you understand the differences in these two situations.

First situation:

________________________________________________________________________________________________________________________________________________________________________________________________

Second situation:

________________________________________________________________________________________________________________________________________________________________________________________________

In the previous situation, you considered the rate of increase in a population as a function of the carrying capacity. Now let us consider a more complete circumstance by beginning with a founder population of 20 prairie dogs that have crossed a dry creek bed due to a temporary dam that was formed by a mudslide upstream. The area being populated contains predators consisting of a few foxes, coyotes, and black footed ferrets.

Use the data provided below to graph the growth of the population that arises from the 20 founders. The long vertical axis (ordinate) will represent the population size at any particular time with one small square representing 20 dogs & the short horizontal axis (abscissa) will represent time from colonization by the founders with five small squares representing 4 months interval.

Months	Population Size
0	20
4	48
8	78
12	262
16	772
20	820
24	844
28	804
32	848

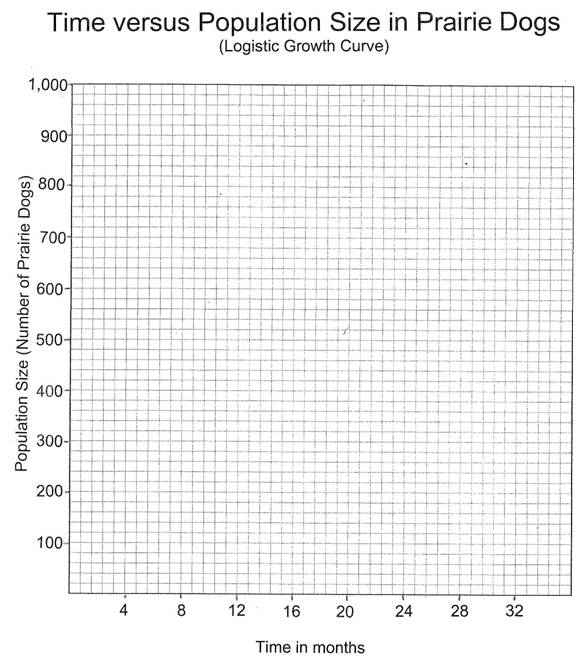
You have constructed a graph of the logistic growth model. The logistic growth curve consists of four phases: lag phase, acceleration phase, deceleration phase, & equilibrium phase. Label these phases on your graph.

Lag phase. This phase occurs during early growth. This initial lag results from the fact that the organisms need to adjust to their new environment. For example, when a natural mammalian population is introduced into a new habitat, it takes time for individuals to locate mating partners. Or when yeast are introduced into culture tubes, it takes time for new enzymes to be synthesized before the cells divide.

Acceleration phase. After the adjustment period, population size increases more & more rapidly (accelerates). During this phase environmental resources are essentially unlimited so that the rate of increase is limited only by the organism’s physiological capacity to survive & reproduce.

Decelerating phase. As the environment starts to become saturated with individuals, the rate of growth progressively declines (decelerates). The rate of growth declines as the birth rate decreases & the death rate increases. In metazoan populations this occurs, for example, as the population size becomes so large that individuals start to compete for space & food. Then certain females may not get enough food to provide energy for successful reproduction, or certain individuals may starve to death. In yeast, the accumulation of waste products may limit growth.

Equilibrium phase. This final phase is reached when the environment becomes saturated with individuals. Now a balance (equilibrium) has been reached between the inherent capacity of the population to increase & the limits imposed on growth by the shortage of environmental resources or by accumulation of waste products. By definition, equilibrium is reached when the birth rate declines to such a point that it becomes equal to the increasing death rate.